|
||||||
Анализатор электрических цепей "Вулкан-2001"
![]()
Описание и руководство по использованию.
Изложенное описание и программное обеспечение являются интеллектуальной собственностью автора. При отсутствии предварительно полученного письменного разрешения категорически запрещено любое их распространение (за исключением инсталляционных пакетов Shareware-версий программы).
Приводятся теоретические сведения, основы алгоритмов, конкретные примеры расчетов. Для радиолюбителей, инженеров, студентов радиотехнических специальностей.
От автора:
Как рассчитать емкость конденсатора, который необходимо подключить к вентилятору 1,0-ЭВ-1,4-4-3270, чтобы напряжение на вентиляторе стало в 2 раза меньше и он не сильно шумел при работе?
Как рассчитать сложный полосовой фильтр из 29 радиоэлементов? Как изменится форма его АЧХ, если изменить номиналы некоторых емкостей?
На некоторые вопросы можно ответить почти мгновенно, другие требуют большого количества вычислений. Например, можно “на глаз” определить порядок токов статического режима 3-каскадного транзисторного усилителя, но для получения точных значений нужно решить систему из 14 уравнений, прежде чем получить ответ…
Если составить таблицу эффективности использования мускульной энергии, на первом месте окажется кондор – он почти не шевелит крыльями при полете. Человек занимает место в нижней трети списка. Но если человеку дать велосипед, то он окажется на первом месте. Стив Джоббс в связи с этим высказался о персональных компьютерах, как о “велосипедах для интеллекта”.
Итак, нажмем на педали!
1. Базовые принципы, используемые в программе.
Для анализа электрических цепей воспользуемся некоторыми топологическими понятиями:
ветвью
узлом
В зависимости от схемы, между двумя произвольными узлами может содержаться либо одна, либо несколько, либо ни одной ветви, а каждая ветвь может содержать либо один, либо несколько элементов. Все элементы
Z, R, X; Y, G, B; L; C; E; J, входящие в ветвь, являются идеальными. Если необходимо учесть реальную паразитную емкость, активное сопротивление провода катушки и т.д., то в схему вводятся соответствующие идеальные элементы паразитной емкости, сопротивления и т.д.Распространены следующие методы расчета электрических цепей:
С применением уравнений Кирхгофа (оба закона).
Метод узловых потенциалов (1-й закон Кирхгофа + закон Ома).
Метод контурных токов (2-й закон Кирхгофа + закон Ома).
Метод расширенных узловых уравнений.
Характерные особенности названных методов указаны в табл. 1:
Таблица 1.
|
Номер |
Количество |
Ограничения на типы элементов |
Метод получения системы независимых уравнений |
|
(1) |
2 * (количество ветвей) |
Нет |
Топологически |
|
(2) |
(количество узлов) - 1 |
Идеальн. E (G=¥ ) |
Непосредственно по схеме |
|
(3) |
(ветви) – ((узлы) – 1) |
Идеальн. I (R=¥ ) |
Топологически |
|
(4) |
(узлы) – 1 + ( r_ветви) |
Нет |
Непосредственно по схеме |
С точки зрения наглядности отражения сути физических процессов, протекающих в схеме, более предпочтителен метод контурных токов (3). Однако применение топологических алгоритмов для формирования системы независимых уравнений значительно усложняет автоматизацию формирования матрицы контурных сопротивлений, что приводит к увеличению размера и уменьшению скорости работы программы. (Для построения матрицы контуров необходим поиск независимых замкнутых контуров графа схемы, то есть имеющих хотя бы одну ветвь связи – хорду, не входящую во все другие контуры и не получающуюся путем удаления из имеющихся контуров общих ветвей.) По этой же причине нецелесообразно использовать расчет с применением законов Кирхгофа (1).
Наиболее часто в литературе встречается использование метода узловых потенциалов (2) в связи с легкостью формирования системы уравнений для решения. Однако и этому методу присущ недостаток – наличие ограничения – схема не должна содержать идеальных источников Э.Д.С. Поэтому необходимо их предварительно вручную пересчитывать в источники тока. Такой подход неприемлем – работая с компьютером, параллельно считать на калькуляторе. В то же время, используя метод расширенных узловых уравнений (4), можно автоматизировано сформировать матричные уравнения и избежать ограничений на типы используемых элементов, незначительно увеличив количество уравнений в решаемой системе по сравнению с методом узловых потенциалов (2).
При использовании метода расширенных узловых уравнений, электрическая схема рассматривается состоящей из т. наз.
g- и r- ветвей, для которых выполняется: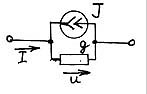
I=gU-J
и
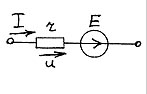
U=rI-E соответственно.
Ветвь идеального источника Э.Д.С. E при этом пусть считается r- ветвью, у которой r = 0. Следовательно, для уменьшения количества уравнений в системе (4, табд.1), целесообразно определять как r- ветвь только идеальные источники Э.Д.С. E.
Таким образом, при использовании метода расширенных узловых уравнений, расчет схемы сводится к решению матричного расширенного узлового уравнения:
|
G(y) Ar |
|
j |
|
J(y) |
|
|
|
x |
|
= |
|
|
|
-ArT r |
|
Ir |
|
E |
|
Для решения составленной таким образом системы линейных алгебраических уравнений целесообразно применить метод Холесского (Кроута) из соображений:
устойчивости метода при расчете разреженных матриц [имеющих большинство нулевых членов](к примеру, метод Гаусса в таком случае часто выходит на деление на ноль или дает недопустимо большие погрешности);
минимальности требований к объему оперативной памяти компьютера и продолжительности вычислений.
В общем случае, для расчета цепей, содержащих линейные и нелинейные элементы, нельзя применить одинаковые принципы (табл.2):
Таблица 2. Применяемость расчетных принципов.
|
|
Линейные цепи |
Нелинейные цепи |
|
Основанных на 1-м законе Кирхгофа |
+ |
+ |
|
Основанных на 2-м законе Кирхгофа |
+ |
+ |
|
Основанных на законе Ома |
+ |
- Вместо закона Ома для нелинейного элемента необходимо пользоваться нелинейной зависимостью I(U) или U(I) |
Однако, один и тот же радиотехнический элемент может быть представлен разными моделями в зависимости от конкретных условий задачи и методов ее решения. Например, транзистор – нелинейный элемент, но если он работает в режиме, когда рабочая точка находится в пределах линейного участка вольт-амперной характеристики (ВАХ) или же на нелинейном участке ВАХ, но анализируемый интервал так мал, что изменение линейности ВАХ пренебрегаемо незначительно, - то при расчетах возможно использовать линейную модель.
*) Линейными цепями называются цепи, для которых зависимости между напряжениями, токами, зарядами и магнитными потоками выражаются линейными функциями
u = R * i; q = C * u; u = Um * sin w t; i = C * du/dt и т.д., а параметры R, С, … - постоянные или изменяются во времени по заданному закону. Нелинейные цепи содержат элементы, которые не могут быть описаны при помощи постоянных коэффициентов, параметры являются нелинейными функциями одной или нескольких переменных: C = B(t) * x + A * x2 .Следовательно, для анализа нелинейной цепи возможно выбрать достаточно малый анализируемый интервал значимого параметра, в пределах которого характеристики цепи будут практически линейными.
На таком подходе построен принцип расчета нелинейных цепей методом последовательных интервалов, сущность которого заключается в замене дифференциальных уравнений алгебраическими, содержащими приращения определяющих величин за соответствующие интервалы времени и расчете изменения исследуемых величин за необходимый временной период (т.е. используется малый параметр и условная линеаризация).
В этом случае уравнения, описывающие цепь, не будут содержать нелинейные операции над переменными и расчет режима цепи сведется к наиболее часто встречающейся в инженерной практике задаче решения системы (ряда систем с приращением аргументов) линейных алгебраических уравнений.
2. Формирование матрицы расширенных узловых уравнений.
2.1. Формирование матрицы узловых проводимостей.
По горизонтали и по вертикали размер матрицы равен числу узлов схемы.
В каждом элементе главной диагонали матрицы должна находиться сумма проводимостей ветвей, соединенных одним концом (полюсом) в соответствующем узле - собственные узловые проводимости. Во всех остальных ячейках должны размещаться отрицательные суммы тех проводимостей, которые расположены между соответствующими узлами - взаимные проводимости.
|
|
Узлы |
1 |
2 |
3 |
|
|
1 |
S |
- Gвз |
- Gвз |
|
G(y) = |
2 |
- Gвз |
S |
- Gвз |
|
|
3 |
- Gвз |
- Gвз |
S |
Пусть имеется проводимость некоторой ветви
G23. Согласно вышеуказанному, ее значение должно добавиться со знаком “+” в ячейки (2,2) и (3,3) и со знаком “-” в ячейки (2,3) и (3,2).Рассматривая таким образом проводимость каждой ветви, а в конечном счете – и проводимость каждого элемента
G, параллельно включенного в ветвь, можно составить полную матрицу узловых проводимостей схемы, заполняя ячейки матрицы по приведенному алгоритму:
- Gmm = Gmm + G элемента, включенного между узлами m и n;
- Gnn = Gnn + G элемента, включенного между узлами m и n;
- G mn = Gmn – G элемента, включенного между узлами m и n;
- Gnm = Gnm - G элемента, включенного между узлами m и n.
Для получения системы из линейно независимых уравнений, матрица
G должна иметь размерность (U-1;U-1), где U- количество узлов в схеме. Её можно получить из сформированной матрицы G(U,U) вычеркиванием старших по номеру столбца и строки, при этом потенциал вычеркнутого старшего по номеру узла примется равным нулю. В принципе, для получения системы независимых уравнений, из матрицы проводимостей G(U,U) можно вычеркнуть строку и столбец, соответствующие номеру любого узла. Но для практических целей лучше начинать нумерацию узлов с единичного и последним нумеровать узел, соответствующий “земле” на схеме:|
|
|
1 |
2 |
… |
U |
|
|
1 |
|
|
|
- |
|
G(y) = |
2 |
|
|
|
- |
|
|
… |
|
|
|
- |
|
|
U |
- |
- |
- |
- |
2.2. Формирование вектора
J узловых токов g- ветвей.Размерность вектора
J: (1;U-1) – получается из вектора J(U) вычеркиванием старшего по номеру элемента (необходимость этого объяснена выше).Выберем систему обозначения токов и Э.Д.С. для вычисления алгебраической суммы токов, присоединенных к данному узлу: со знаком “+” будем записывать токи, входящие в узел, и со знаком “-” - выходящие из него.
- J(k1) = J(k1) + номинал тока;
- J(k2) = J(k2) – номинал тока,
где k1 – номер “плюсового” узла (ток втекает), k2 – номер “минусового” узла (ток вытекает. Рассматриваются узлы одной ветви, через которую протекает ток указанного номинала).
|
|
1 |
J1(y) |
|
|
2 |
J2(y) |
|
J = |
… |
… |
|
|
U |
Ju(y) |
2.3. Формирование вектора Е Э.Д.С.
r- ветвей.Размерность вектора
E: (1; r), где r – количество r- ветвей, то есть Э.Д.С.E(r) = | номинал |;
|
|
1 |
|E1| |
|
|
2 |
|E2| |
|
E = |
… |
… |
|
|
r |
|Er| |
2.4. Формирование матрицы
A соединений r- ветвей.Размерность матрицы
A: (U-1; r) – получается вычеркиванием старшей строки из матрицы A(U; r).Т.к. ранее мы приняли, что
r- ветвями мы будем считать только идеальные Э.Д.С. и при вводе позициям “начало(+)” соответствует “+” Э.Д.С., а “конец(-)” – соответствует “-” Э.Д.С., то:|
|
0, если узел не k1 и не k2 |
|
A(i;j) = |
1, если узел = k2 |
|
|
-1, если узел = k1 |
|
|
|
r- ветви |
|
|
У |
… |
|
A = |
З |
… |
|
|
Л |
… |
|
|
Ы |
… |
2.5. Формирование матрицы R сопротивления
r- ветвей.Исходя из принятого, что
r- ветвями являются только идеальные источники Э.Д.С., имеющие внутреннее сопротивление равное нулю, матрица R также получится нулевой и необходимость ее формирования отпадает.3. Немного математики.
Для получения возможности расчета АЧХ, ФЧХ и
Zвх анализируемых цепей, необходимо расчет системы полученных уравнений производить в комплексных коэффициентах. Для этого вспомним некоторые математические моменты.Синусоидальное колебание переменного тока или напряжения можно представить формулой:
A = Am * sin (w t + j ) = Am * sin [w * (t + j /w )],
где Am – максимальная амплитуда;
w - циклическая частота;
j - начальный угол сдвига фазы.
При этом:
w = 2 * p * f = 2 * p / T;
f = 1 / T.
Колебание такого вида на комплексной плоскости может быть представлено вращающимся против часовой стрелки вектором
Am.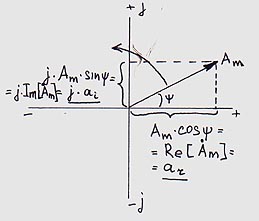
Координаты точки, описываемой вращающимся вектором Am, могут быть представлены в различных системах. С точки зрения удобства восприятия наиболее выгодным представляется способ записи в полярных координатах (полярная форма), а с точки зрения удобства программирования расчета – в декартовых координатах (алгебраическая форма записи комплексных чисел).
Существуют определенные правила выполнения математических операций над комплексными числами. Запишем их в алгебраической форме для чисел
a и b (r и i – соответственно индексы реальной и мнимой составляющей комплексного числа):a + b = (ar + br) + j * (ai + bi);
a – b = (ar – br) + j * (ai – bi);
a * b = (arbr – aibi) + j * (arbi + aibr);
a / b = (arbr + aibi) / (br2 + bi2) + j * ((aibr – arbi) / (br2 + bi2));
1 / a = ar / (ar2 + ai2) – j * (ai / (ar2 + ai2)).
Видно, что для выполнения математических операций над комплексными числами необходимо обрабатывать два массива – для реальных и мнимых частей, над которыми для получения результата можно производить раздельно математические операции. Это используется в программе.
Переход от алгебраической формы к полярной весьма прост:
A = Ö (ar2 + ai2);
y = arctg (ai / ar).
Вспомним некоторые моменты теории цепей:
Для составления матрицы узловых проводимостей определим комплексные проводимости элементов R, C, L:
YR = 1 / R;
YC = jw C;
YL = - j / w L.
Комплексная проводимость ветви, составленной из элементов
R, C, L:Y = YR + YC + YL.
Комплексная передаточная функция (КПФ) определяется, как отношение комплексной выходной величины ко входной. КПФ может определяться по напряжению, току, проводимости, сопротивлению, - в зависимости от того, какие величины приняты за выходные и входные.
K = Aвых / Aвх.
Зависимость модуля комплексной передаточной функции от частоты называется амплитудно – частотной характеристикой (АЧХ):
K(f) = Ö (Kr2(f) + Ki2(f)).
Если передаточная функция вычисляется по току или напряжению, можно составить логарифмические АЧХ в децибелах или Неперах:
D(f) = 20 * lg K(f) [дБ];
N(f) = ln K(f) [Нп];
1 Нп » 8,69 дБ.
Зависимость аргумента комплексной передаточной функции от частоты называется фазо – частотной характеристикой (ФЧХ):
Y (f) = arctg (Ki(f) / Kr(f)).
Комплексное входное сопротивление может быть получено аналогично комплексной передаточной функции, если выходные выводы принять совпадающими со входными. Соответственно можно получить зависимсости модуля и аргумента комплексного входного сопротивления от частоты, то есть входного сопротивления и его фазы. Кроме того,
Zвх = Uвх / Iвх
4. Описание работы с программой и примеры.
Анализ приведенных в литературе программ приводит к выводу об устанавливаемых ими ограничениях на типы элементов вследствие выбранного метода анализа (практически все программы основываются на методе узловых потенциалов), что подразумевает хорошее знание пользователем теории электрических цепей для ввода элементов с ограничениями. Либо же программы пишут, привязываясь к конкретной схеме – активный фильтр на операционном усилителе; транзисторный усилительный каскад, включенный по схеме “с общим эмиттером” и т.п. Либо же в импортных программах (типа
Electronic Workbench) неясно вообще какие необходимо ввести параметры отечественных полупроводниковых приборов для правильного расчета, так как не описываются используемые алгоритмы расчетов. Эти факторы значительно снижают эффективность применения в повседневной практике таких автоматизированных методов расчета электронных схем. Предлагаемая программа рассчитана на эффективное использование как начинающими радиолюбителями, так и квалифицированными инженерами. В ней сняты ограничения на типы источников электроэнергии. Табличное представление данных, выводы графиков с автоматическим масштабированием по осям, использование экономичных по требуемому объему памяти и оптимальных по скорости вычислений алгоритмов, четкое структурное построение программы позволит Вам ее применять, как эффективного помощника в работе.4. Статический режим.
4.1. Зависимых источников тока и напряжения нет.
Схема № 1.
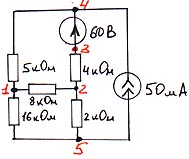
Здесь и далее в первую очередь расставляем узлы таким образом, чтобы каждая ветвь содержала один идеальный элемент, а номер последнего узла по возможности соответствовал “земле”. Между одними и теми же двумя узлами может быть без проблем включено несколько ветвей. Если ветвь содержит несколько идеальных элементов, разбейте ее на несколько последовательно включенных ветвей, расставив между элементами точки узлов.
Запускаем анализатор “Вулкан”.
Выбираем в верхнем меню: Файл – Новый.
В появившемся окне вводим имя расчета “Схема № 1”.
В появившемся окне вводим количество узлов: 5.
Вводим элементы по очереди в таблицу ввода:
E 1 4 3 60 *)острие стрелки Э.Д.С. соответствует “+, начало”
J 1 4 5 50E-3 *)то же для идеального источника тока; степенные
R 1 1 4 5000 показатели в программе вводятся английской буквой
R 2 1 5 16000 E с указанием степени основания 10.
R 3 1 2 8000
R 4 2 3 4000
R 5 2 5 2000
Нажимаем кнопку “Статика” – появляется окно с результатами расчета:
U(1) = 160
U(2) = 79.99999
U(3) = 200
U(4) = 260
I(1) = -0.03
Таким образом, мы получили значения напряжения в точках, соответствующих номерам узлов, а также ток через имеющийся в схеме идеальный источник Э.Д.С.
Не забывайте, что после каждого появления окна с результатами расчетов (в любом из режимов работы программы), Вы можете скопировать данные расчета из файла С:\Мои документы\crntdata
.vlc в необходимое место (только если запущен Проводник, не забывайте сделать Вид-Обновить).Далее Вы можете закрыть окно результатов расчета кнопкой “Закрыть” на нем или очистить его содержимое кнопкой “Очистить” или просто переключиться опять на окно анализатора, при необходимости изменить значения каких-либо элементов и рассчитать статику опять. Если при этом окно результатов не закрывать и не очищать, то в нем также будут видны результаты предыдущих расчетов.
Схема № 2.
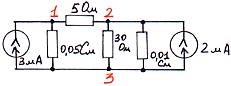
Таблица ввода:
G 1 1 3 0.05
G 2 2 3 0.01
J 1 1 3 3E-3
J 2 2 3 2E-3
R 1 1 2 5
R 2 2 3 30
Клацаем по “Статике”, получаем результаты расчета:
U(1) = 0.05424
U(2) = 0.0528
Потенциал третьей точки, из сказанного выше, равен нулю. Естественно, зная приложенное к ветви напряжение, когда это нужно, можно вычислить ток через ветвь, разделив разность узловых напряжений на сопротивление ветви.
4.1.3. Схема № 3.
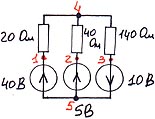
Таблица ввода:
E 1 1 5 40 *)не забываем правильно указывать начало и конец
E 2 2 5 5 источников (то есть полярность их включения)
E 3 5 3 10
R 1 1 4 20
R 2 2 4 40
R 3 3 4 140
Результаты расчета
:U(1)=40
U(2)=5
U(3)=-10
U(4)=25
I(1)=0,75
I(2)=-0,5
I(3)=0,25
Конечно, везде все номиналы стандартные – Амперы, Вольты, Омы, Сименсы, Генри, Фарады.
4.1.4. Схема № 4.
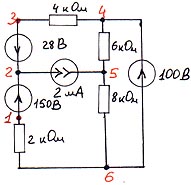
Таблица ввода:
E 1 2 1 150
E 2 2 3 28
E 3 4 6 100
J 1 5 2 2E-3
R 1 1 6 2000
R 2 3 4 4000
R 3 4 5 6000
R 4 5 6 8000
Результаты расчета:
U(1)=-10
U(2)=140
U(3)=112
U(4)=100
U(5)=64
I(1)=4,999999E-03
I(2)=-2,999999E-03
I(3)=0,003
4.1.5. Схема № 5.
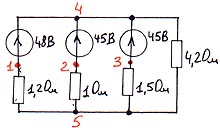
Таблица ввода:
E 1 4 1 48
E 2 4 2 45
E 3 4 3 45
R 1 1 5 1.2
R 2 2 5 1
R 3 3 5 1.5
R 4 4 5 4.2
U(1)=-6
U(2)=-3
U(3)=-3
U(4)=42
I(1)=5,000001 (выскочила погрешность, т.к. в Shareware версии - переменные одинарной
I(2)=3 точности)
I(3)=2
Статический режим с зависимыми источниками тока и напряжения.
Схема № 10.
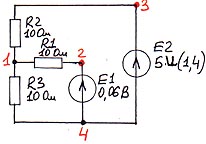
Таблица ввода:
E 1 2 4 0.06
E 2 3 4 5 ИНУН 1 4
R 1 1 2 10
R 2 1 3 10
R 3 1 4 10
Здесь мы впервые используем ввод в графу “Подпр(ограмма)” и “Упр(авляющий узел 1, начало, +)” и “Упр(авляющий узел 2, конец, -). Так как управляемый источник в схеме – Источник Напряжения, Управляемый Напряжением, выбираем ИНУН и указываем, что его значение зависит от напряжения между узлами 1 и 4, а значение его получается умножением напряжения между узлами 1 и 4 на коэффициент 5.
Кроме ИНУН, возможны:
ИНУТ – источник напряжения, управляемый током;
ИТУН – источник тока, управляемый напряжением;
ИТУТ – источник тока, управляемый током.
Активные усилительные элементы могут представляться такими зависимыми источниками. Так, биполярный транзистор представляет собой ИТУТ; полевой транзистор либо ИТУН либо ИНУН; усилительная лампа ИНУН; операционный усилитель чаще всего ИНУН и т.п. в зависимости от особенностей управляемого источника.
Результаты расчета:
U(1)=-0,03
U(2)=0,06
U(3)=-0,15
I(1)=9,000001E-03
I(2)=-0,012
4.2.2. Схема № 11.
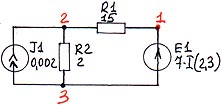
Таблица ввода:
E 1 1 3 7 ИНУТ 2 3
J 1 2 3 0.002
R 1 1 2 15
R 2 2 3 2
Результаты расчета:
U(1)=0,021
U(2)=6,000001E-03
I(1)=0,001
4.2.3. Схема № 12.
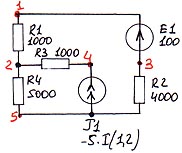
Таблица ввода:
E 1 1 3 100
J 1 4 5 -5 ИТУТ 1 2
R 1 1 2 1000
R 2 3 5 4000
R 3 2 4 1000
R 4 2 5 5000
Результаты расчета:
U(1)=126,6667
U(2)=133,3334
U(3)=26,66671
U(4)=166,6667
I(1)=-6,666677E-03
4.2.4. Схема № 13.
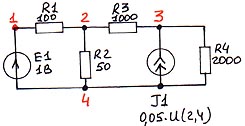
Таблица ввода:
E 1 1 4 1
J 1 3 4 0.05 ИТУН 2 4
R 1 1 2 100
R 2 2 4 50
R 3 2 3 1000
R 4 3 4 2000
Результаты расчета:
U(1)=1
U(2)=-3,333331
U(3)=-113,3332
I(1)=4,333331E-02
4.2.5. Схема № 14.
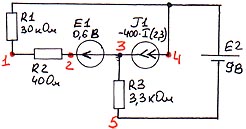
Таблица ввода:
E 1 2 3 0.6
E 2 4 5 9
J 1 3 4 -400 ИТУТ 2 3
R 1 1 4 30000
R 2 1 2 40
R 3 3 5 3300
Результаты расчета:
U(1)=1,441511
U(2)=1,431433
U(3)=0,8314326
U(4)=9
I(1)=-2,519493E-04
I(2)=2,519496E-04
Расчет узловых напряжений в комплексных коэффициентах.
Схема № 6.
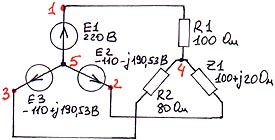
Таблица ввода:
E 1 1 5 220
E 2 2 5 -110 -190.53
E 3 3 5 -110 190.53
R 1 1 4 100
R 2 3 4 80
Z 1 2 4 100 20
*) Значения Е1..Е3 соответствуют фазным напряжениям трехфазной сети 220 В. Для других n-фазных напряжений см.п. 3 с учетом фазового сдвига 360/n.
Клацаем по кнопке “
U узл.”, что означает узловые напряжения в комплексных коэффициентах. Получаем значения:U(1)=220 j0
U(2)=-110 j-190,53
U(3)=-110 j190,53
U(4)=-20,00195 j22,50258
I(1)=2,40002 j-0,2250258
I(2)=-1,275044 j-1,875317
I(3)=-1,124976 j2,100343
Сразу видно, что фазы нагружены неравномерно – в точке 4 существует перекос напряжения 20+
j22,5 В.
4.3.2. Схема № 7.
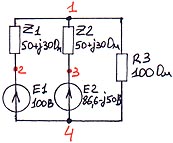
Таблица ввода:
E 1 2 4 100
E 2 3 4 86.6 -50
R 3 1 4 100
Z 1 1 2 50 30
Z 2 1 3 50 30
Клацаем по кнопке “
U узл.”, получаем результаты:U(1)=71,21452 j-28,54574
U(2)=100 j0
U(3)=86,6 j-50
I(1)=0,6751903 j0,1658007
I(2)=3,695496E-02 j-0,4512582
Динамические режимы.
5.1. Расчет АЧХ.
5.1.1. Схема ФНЧ на стр. 135 книги В.Т.Полякова “Радиолюбителям о технике прямого преобразования”.
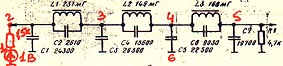
*) при расчетах динамических режимов в обязательном порядке нужно, чтобы на вход схемы подавался сигнал, который затем будет анализироваться на выходе. В приведенной схеме фильтра вход “висит”, поэтому подключим к нему источник Э.Д.С. с условным номиналом 1 В с последовательно включенным сопротивлением 1500 Ом, что примерно соответствует выходу предыдущего транзисторного усилительного каскада.
Таблица ввода:
C 1 2 6 24300E-12
C 2 2 3 2610E-12
C 3 3 6 26300E-12
C 4 3 4 13600E-12
C 5 4 6 22500E-12
C 6 4 5 9030E-12
C 7 5 6 19700E-12
E 1 1 6 1
L 1 2 3 0.231
L 2 3 4 0.146
L 3 4 5 0.168
R 1 5 6 4700
R 2 1 2 1500
Клацаем по кнопке “АЧХ”, появляется окно ввода параметров динамических режимов.
Вводим:
Частота начала расчета – 100 Гц, конец расчета – 15000 Гц, шаг по частоте – 100 Гц.
*) Вы всегда можете более подробно и более крупным планом посмотреть заинтересовавший Вас участок АЧХ, если сделаете меньшим диапазон, в котором производится расчет и меньшим шаг по частоте. Так как комплексная передаточная функция является отношением выходного сигнала ко входному, определяем входы и выходы, для которых будет рассчитана АЧХ:
Вход +: 2
Вход -: 6
Выход +:5
Выход -:6
Отмечаем птичкой окошко “Вывести график” и переключаем на “Логарифмический по значению
Y”.Клацаем по кнопке “Ввод значений” на этом окне. Происходит расчет и появляются два окна – “Результаты расчета” и “График”. Шаг расчета по частоте на графике откладывается точками, то есть если расчет начинался со 100 Гц, то значению АЧХ при 100 Гц соответствует точка графика, лежащая на оси
Y; для 200 Гц – первая красная точка, для 300 Гц – вторая красная точка и т.д.Иногда число точек расчета задается настолько большим, что красные точки сливаются в линии и по ним невозможно отсчитать частоту. В этом случае нужно либо просмотреть окно с численными данными “Результаты расчета” либо закрыв окно “График”, повторно пересчитать АЧХ, задав больший шаг по частоте.
Конечно Вы имеете возможность в окне анализатора изменить номиналы элементов и пересчитать схему заново. Учтите при этом, что если окно “График” не закрывалось, то в нем есть старый график и дополнительно происходит построение нового только что рассчитанного. Это удобно для качественного сравнения, но не позволяет сравнить значения количественно, так как для каждого вывода графика производится автоматическое масштабирование от минимального значения до максимального, то есть меняется масштаб по оси
Y. Если Вам нужно построить графики в одном масштабе, то необходимо сделать первый расчет, из файла С:\Мои документы\crntdata.vlc перенести данные в Word, выделить все, преобразовать в таблицу ( меню Таблица – Преобразовать в таблицу, выбрав в качестве разделителя точку с запятой), выделить все и скопировать в Excel. То же самое сделать для второго расчета, и далее из данных построить необходимые графики, пользуясь средствами Excel.Рассчитанная нами АЧХ (график построен в
Excel) имеет вид: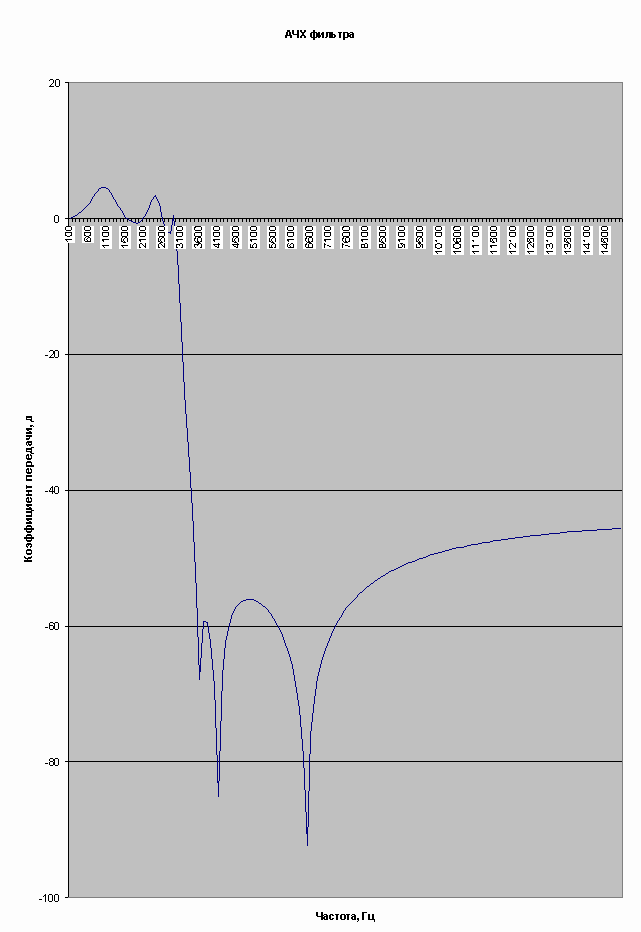
Что в принципе хорошо согласуется с приведенным в книге Полякова графиком затухания, то есть зеркально симметричному графику пропускания:
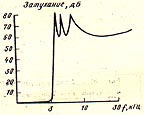
Однако, на нашем графике видно, что в полосе пропускания фильтр имеет неравномерность АЧХ от (смотрим в полосе до 3 кГц в окне результатов расчета) +4,59 дБ на частоте 1000 Гц до –4,28 дБ на частоте 2600 Гц, то есть разброс амплитуды в полосе пропускания составляет в сумме 8,87 дБ – это не очень здорово, т.к. в радиотехнике принято, что разброс значений АЧХ в пределах полосы пропускания не должен составлять более 3 дБ.
Кроме того, по графику (и по результатам расчета) видно, что после пиков затухания у фильтра существует асимптотический рост до уровня около –43 дБ в полосе задерживания, что в целом не так уж плохо.
Поляков приводит данные, что частоты бесконечного затухания составляют 3,6; 4,1 и 6,5 кГц. Произведя расчет АЧХ в диапазоне 3-7 кГц с шагом в 1 Гц, пользуясь окном “Результаты расчета”, уточним, что точное значение этих частот 3572 Гц, 4086 Гц и 6482 Гц.
Уточнять можно и далее до необходимой точности. Например, просчитав АЧХ от 3570 до 3575 Гц с шагом 0,001 Гц, уточним значение частоты бесконечного затухания
- 3571,694 Гц.Так что можно с полным основанием сказать, что Поляков – молодец и фильтр в целом неплохой.
Расчет ФЧХ.
5.2.1. Схема пассивного
RC фазовращателя на стр. 158 книги В.Т.Полякова “Радиолюбителям о технике прямого преобразования”.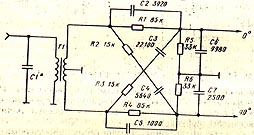
Для расчета заменим вторичную обмотку трансформатора двумя идентичными ЭДС:
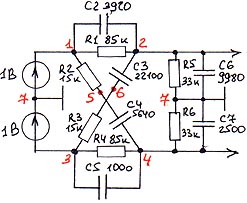
Таблица ввода:
C 2 1 2 3920E-12
C 3 2 6 22100E-12
C 4 5 4 5640E-12
C 5 3 4 1000E-12
C 6 2 7 9980E-12
C 7 4 7 2500E-12
E 1 1 7 1
E 2 7 3 1
R 1 1 2 85000
R 2 1 5 15000
R 3 3 6 15000
R 4 3 4 85000
R 5 2 7 33000
R 6 4 7 33000
Клацаем по кнопке “ФЧХ”, в появившемся окне вводим данные частот: от 400 Гц до 3500Гц с шагом в 100 Гц; входы 1 и 7; выходы 2 и 7. Выбираем “линейный” график (иначе в окне результатов расчета получи логарифм сдвига фазы), нажимаем “ввод значений” - производится расчет. Видно, что фаза по частоте изменяется значительно.
Делаем такой же расчет для выходов 4 и 7. Через
Excel вычисляем разницу соответствующих значений фазы на выходах 2 и 4. Получаем таблицу: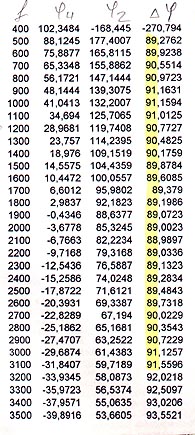
Не стоит пугаться первого значения –270,794. Просто прибавим 360 градусов и получим 89,206 градусов. Как и пишет Поляков, точность фазового сдвига для диапазона частот 300 Гц…3кГц составляет 1%. В нашей таблице видно, что больше 1 % фазовый сдвиг становится равным от частоты 3 кГц и выше. Также видно, что фаза на обоих выходах в указанном диапазоне изменяется значительно, но разница фаз остается постоянной.
Расчет входного сопротивления.
Порядок ничем не отличается от порядка расчета для других динамических режимов. Следует обратить внимание на то, что входное сопротивление будет рассчитываться для узлов “Входы”. Узлы эти могут быть любыми. Не забывайте, что сопротивление источников ЭДС по умолчанию равно нулю. Естественно, для расчета входного сопротивления после ввода элементов в таблицу, нужно нажимать кнопку “
Zвх”.
Схемы замещения.
Радиотехнические элементы и электронные приборы могут быть классифицированы по следующим свойствам:
инерционность (безынерционные: Авых
стационарность (стационарные: Авых =
линейность (линейные
На основании этого может быть создано множество моделей радиоэлементов в зависимости от конкретных условий (диапазон частот, амплитуда сигнала и т.п.).
6.1. Базовые схемы замещения управляемых источников.
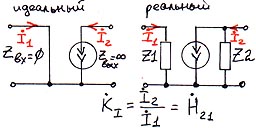
6.1.1. ИТУТ.
Источник тока, управляемый током.
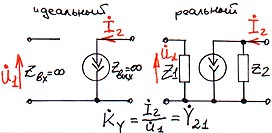
6.1.2. ИТУН.
Источник тока, управляемый напряжением.
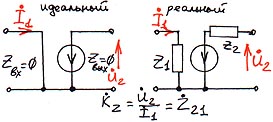
6.1.3. ИНУТ.
Источник напряжения, управляемый током.
6.1.4. ИНУН.
Источник напряжения, управляемый напряжением.
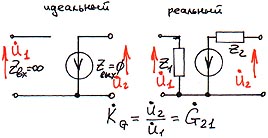
Диод.
Для статического режима существенно диф. сопротивление и напряжение отпирания диода. Для динамического – диф. сопротивление и емкость перехода.
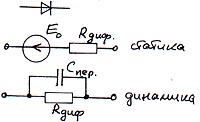
Биполярный
Первое, что хочу сказать – это то, что Вы самостоятельно можете создавать и модифицировать любые модели в зависимости от особенностей расчета. Ясно, что для ВЧ-транзистора будут играть роль паразитные емкости переходов, индуктивности выводов и т.п. То есть, если Вы в справочнике обнаружили к примеру, величину паразитной емкости, можете смело добавлять ее в виде отдельного идеального элемента – конденсатора к необходимым выводам. Однако не всегда целесообразно использовать максимально приближенную к действительности схему замещения активного элемента. К примеру, если Вы рассчитываете активный фильтр на транзисторах для звукового диапазона – в этом случае индуктивность выводов транзистора вообще никакой роли не играет, влияние паразитных емкостей ничтожно и все это можно не вводить в схему замещения. Так же за исключением специальных случае обычно не учитывают потери энергии в диэлектрике конденсаторов, межвитковую емкость и поверхностный эффект в индуктивностях.
Модель для статического режима:
В данной модели учитываются:
входное сопротивление,
напряжение, необходимое для открытия эмиттерного перехода (для вывода рабочей точки транзистора на линейный участок ВАХ),
усилительные свойства транзистора представлены включенным между коллектором и эмиттером источником тока с величиной, равной произведению статического коэффициента передачи тока на ток базы транзистора,
токи утечки.
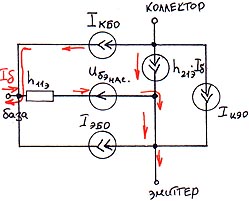
*) токи утечки
Iкбо и Iэбо учитываются редко, можно указанные источники тока из модели исключить.Модель для динамических режимов:
В динамических режимах считаем, что рабочая точка выведена на линейный участок, соответствующим смещением открыт переход база-эмиттер, обратные токи не учитываем. В динамических режимах из источников тока и напряжения в схеме замещения должны остаться только источник, подключенный ко входу схемы (в качестве генератора сигналов) и управляемые источники, которые управляются либо входным сигналом, либо сигналом от другого управляемого источника. Для динамического режима обычно считаем, что цепь питания и “земля” закорочены (по переменному току через емкость фильтров питания большой величины и нулевое сопротивление самого источника ЭДС).
Для малого сигнала в динамическом режиме учитывается только входное сопротивление транзистора и его усилительные свойства, поэтому модель упрощается до вида:
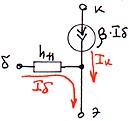
*)Полевые транзисторы можно представлять стандартными ИНУНами, соответственно “обвешав” их паразитными емкостями.
В зависимости от используемой системы параметров, можно строить разные модели:
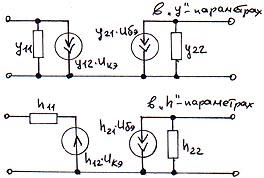
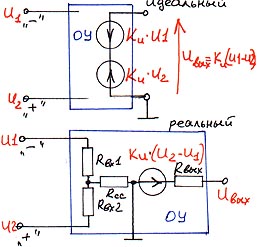
6.2. Операционный усилитель.
Большинство операционных усилителей представляют из себя источники напряжения, управляемые напряжением. Только некоторые ОУ имеют в своем составе выходной усилитель тока.
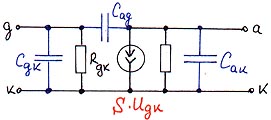
Электронная лампа.
Представляется ИТУНом.
Для динамических режимов учитываем межэлектродные емкости.
Индуктивно связанные элементы.
Последовательно соединенные:
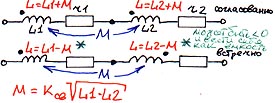
Параллельно соединенные с согласованным включением обмоток (то есть по сути трансформатор без сердечника
) на переменном токе.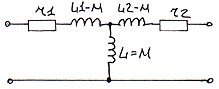
Думаю, не стоит особо разъяснять, что для статики обмотки никак не связаны между собой и моделируются омическим сопротивлением их провода, взаимной индуктивности нет.
6.6. Трансформатор с сердечником.
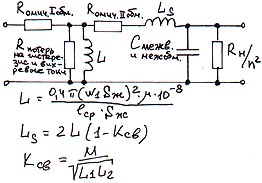
7. Пример расчета статического и динамических режимов реального трехкаскадного усилителя из техники связи.
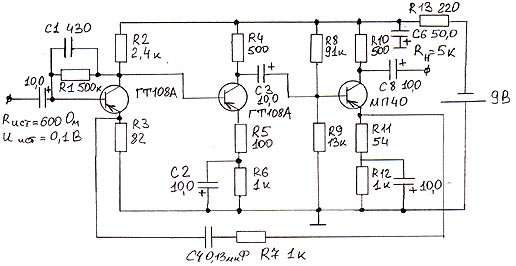
При составлении схемы замещения для статического режима выберем модель транзистора, учитывающую
Uбо, Iкэо, h11, усилительные свойства. Элементы, не влияющие на цепи протекания постоянного тока (емкости), исключим.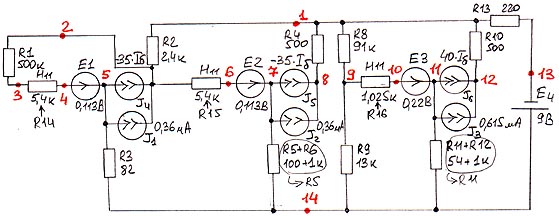
Таблица ввода:
E 1 5 4 0.113
E 2 7 6 0.113
E 3 11 10 0.22
E 4 14 13 9
J 1 2 5 0.00036
J 2 8 7 0.00036
J 3 12 11 0.000615
J 4 2 5 -35 ИТУТ 4 5
J 5 8 7 -35 ИТУТ 6 7
J 6 12 11 -40 ИТУТ 10 11
R 1 2 3 500000
R 10 1 12 500
R 11 11 14 1054
R 13 1 13 220
R 14 3 4 5400
R 15 2 6 5400
R 16 9 10 1025
R 2 1 2 2400
R 3 5 14 82
R 4 1 8 500
R 5 7 14 1100
R 8 1 9 91000
R 9 9 14 13000
Значения
Uбо и Iкэо берем из справочной литературы. Коэффициент усиления транзисторов вводим со знаком минус, так как транзисторы включены по схеме с ОЭ и фаза сигнала на коллекторах изменяется на 180 градусов относительно входного сигнала.Нажимаем кнопку “Статика”, получаем результаты:
U(1)=-8,509719
U(2)=-5,701933
U(3)=-0,2028124
U(4)=-0,1434219
U(5)=-3,042186E-02
U(6)=-1,387804
U(7)=-1,274804
U(8)=-8,32972
U(9)=-0,8984208
U(10)=-0,8835261
U(11)=-0,6635261
U(12)=-8,202219
U(13)=-9
I(1)=-1,099824E-05
I(2)=-7,989127E-04
I(3)=-1,453136E-05
I(4)=2,228553E-03
Обратите внимание, что так как потенциалом “нуля” была принята цепь, подключенная к плюсу источника питания, все напряжения рассчитались относительно нее и имеют знак минус, что означает, что потенциал этих цепей меньше “нулевого”.
При составлении схемы замещения для динамического режима считаем, что соответствующим статическим смещением рабочие точки транзисторов выведены на линейные участки характеристик (открыты переходы база-эмиттер). Учитываем, что емкости больших номиналов представляют из себя почти короткое замыкание для переменного тока и заменяем их просто соединением проводником (хотя конечно же Вы можете просчитать схему со всеми емкостями – составьте для этого соответствующую схему замещения). Следствием этого также является то, что через емкость фильтра цепь, объединяющая резисторы в цепи коллекторов, замыкается по переменному току на корпус.
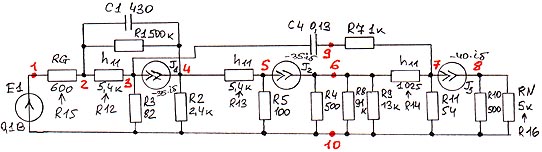
Таблица ввода:
C 1 2 4 430E-12
C 4 3 9 0.13E-6
E 1 1 10 0.1
J 1 4 3 -35 ИТУТ 2 3
J 2 6 5 -35 ИТУТ 4 5
J 3 8 7 -40 ИТУТ 6 7
R 1 2 4 500000
R 10 8 10 500
R 11 7 10 54
R 12 2 3 5400
R 13 4 5 5400
R 14 6 7 1025
R 15 1 2 600
R 16 8 10 5000
R 2 4 10 2400
R 3 3 10 82
R 4 6 10 500
R 5 5 10 100
R 7 7 9 1000
R 8 6 10 91000
R 9 6 10 13000
Рассчитываем АЧХ в диапазоне 100 Гц – 5 кГц. График спадающий, коэффициент усиления на частоте 300 Гц составляет 36,05 дБ, полоса пропускания (если брать падение на 3 дБ от значения коэффициента усиления на частоте 300 Гц, то есть до значения 33,05 дБ) – примерно до 2700 Гц.
8. Список использованной литературы:
8.1. Нереттер В. Расчет электрических цепей на персональной ЭВМ. М., Энергоатомиздат, 1991.
8.2. Зевеке Г.В. и др. Основы теории цепей. М., Энергоатомиздат, 1989.
8.3. Шебес М.Р. и др. Задачник по теории линейных электрических цепей. М., Высшая школа, 1990.
8.4. Дьяконов В.П. Применение персональных ЭВМ и программирование на языке Бейсик. М., Радио и связь, 1989.
Дьяконов В.П. Справочник по алгоритмам и програмам на языке Бейсик для персональных ЭВМ. М., Наука, 1989.
Калабеков Б.А. и др. Методы автоматизированного расчета электронных схем в технике связи. М., Радио и связь, 1990.
Геворкян Г.Х. Электротехнические расчеты на языке Бейсик. М., Энергоатомиздат, 1989.
Шуп Т.Е. Прикладные численные методы в физике и технике. М., Высшая школа, 1990.
Чуа Л.А. Машинный анализ электронных схем. М., Энергия,
От автора всем пожелания здоровья и благополучия.
Я надеюсь, что “Вулкан” по ассоциации с одним из богов Олимпа, который был кузнецом и что-то делал своими руками (остальные в основном занимались интриганством), также поможет Вам что-то рассчитать и сделать своими руками.
Все исходники с комментариями имеются.
Далее буду размышлять о том, как на базе анализатора создать САПР с базами данных по отечественным приборам
и драг-друповской системой рисования схемы, чтобы не вводить таблицу вручную.10.07.01 10:14
Александр Далечин g2@mercury.kherson.ua